Идти вперед. По Гаусса кривой,
Не замечая кривизны излома,
И посмеяться дерзко над собой,
Пока сознанье не охватит кома.
Ирина Горюнова
Один из величайших математиков всех времён, «король математиков», а по совместительству выдающийся астроном и физик восемнадцатого-девятнадцатого веков Иоганн Карл Фри?дрих Га?усс (Johann Carl Friedrich Gau?) ещё будучи студентом колледжа в Брауншвейге (Германия) начал исследования в области так называемого «нормального распределения», названного в последствии его именем. В ходе работы им была выведена кривая Гаусса или просто гауссиана. — симметричная параболическая кривая, которая в большинстве случаев возникает при изображении серии результатов на частотном графике.
Так, например, многие переменные образуют нормальное распределение, когда измерения проводятся в целой популяции. В частности, в результате статистических исследований было выявлено, что рост человека и коэффициент умственного развития при достаточно большом количестве участников абсолютно подчиняются принципу нормального распределения. Другими словами, чем больше мы людей мы будем рассматривать, тем больше среди них окажется индивидуумов среднего роста и средних умственных способностей, а «карликов» и «великанов», или, соответственно, людей с ограниченными умственными способностями и гениев будет меньше.
Публицист Александр Новиков в своей известной книге «Апгрейд обезьяны» отмечает эту тенденцию на ряде примеров:
По гауссиане ложатся снаряды вблизи от точки прицеливания.
По гауссиане распределяется число букв (страниц) в выпускаемых цивилизацией книгах.
По гауссиане распределяется вероятность обнаружения частицы в какой?либо точке пространства (по сути, закон Гаусса – это всего лишь отражение волновой функции микромира в макромире).
По гауссиане распределяется артериальное давление в популяции.
По гауссиане распределяется размер шариков, которые делают на шарикоподшипниковом заводе для подшипников…
и так далее.
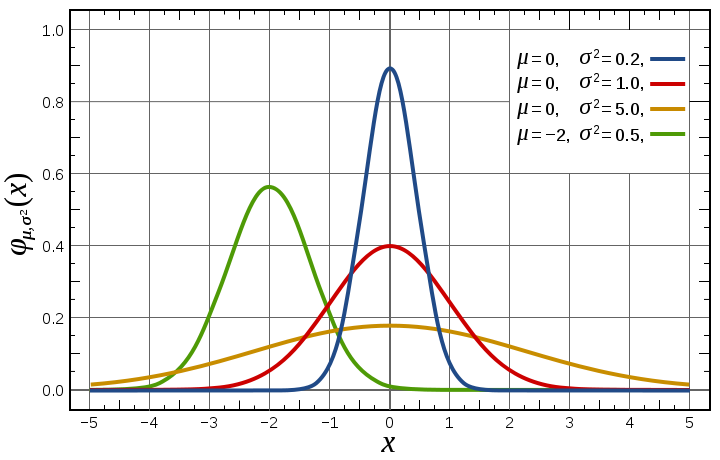
Соответственно большинство результатов на графике кривой Гаусса концентрируется вокруг центра, а наиболее высокие и низкие результаты встречаются гораздо реже. Эти «хвосты» нормального распределения вытягиваются в обоих направлениях вдоль оси абсцисс и теоретически никогда не соприкасаются с нею (см. рисунок 1).
Не буду лукавить, что знал это ранее, или, как вариант, знал, но забыл. Открыть для себя данную информацию меня заставила интересная заметка Игоря Василевского «Гауссиана в продажах». Автор справедливо указывает на тот факт, что при планировании продаж руководители отделов и служб продаж очень часто полагаются на прямую пропорциональность. Это ещё один математический термин, означающий функциональную связь между двумя переменными, которые изменяются в одном и том же направлении: с увеличением (уменьшением) одной переменной увеличивается (уменьшается) и другая переменная. Графически прямая пропорциональность представляет собой прямую линию, проходящую через начало координат.
На языке управляющих продажами это можно описать так:
— чем больше звонков потенциальным клиентам, тем больше встреч;
— чем больше встреч, тем больше контрактов;
— чем больше контрактов, тем больше прибыль,
то есть зависимость, которую мы рассмотрели в статье «Мишка Шифман башковит или сТРуктурА продаж».
Игорь Василевский, соглашаясь с Гауссом в том, что большую часть явлений и процессов во Вселенной, отражает не прямая линия, а гауссиана, распространяет эту тенденцию и на процесс продажи (интересный вывод, требующий осмысления и проверки на практике – Р.Ч.). С одной стороны автор всё же подтверждает рост вероятности положительного результата с ростом числа попыток (то есть, те самые наши заветные «больше звонков – больше встреч»). Но с другой, настаивает на том, что это справедливо только до определенного момента, после которого количество переходит к снижению качества звонков, встреч, прибыли и т. д. Предлагаю коллегам проверить это утверждение при очередном анализе продаж своих компаний и уровня активности подчинённых менеджеров по продажам и проинформировать нас о результатах работы!




22 января, 2015 on 11:10 пп
Проверил уже. С учётом кривой Гаусса. я разрабатывал систему в 2008 году, а вообще система продаж была разработана в 60-ые годы. В 11 уроке курса рассказал , как делал я.
Система продаж для программистов, кому интересно, учитесь
продавать.
2 июля, 2011 on 5:43 пп
http://www.warandpeace.ru/ru/exclusive/view/59499/
Аббе 01.07.11 17:53
Абстрактные понятия с совсем даже реальными последствиями. Помнится в метрологии как производственной отрасли (была такая, правда БЫЛА!) умные люди знали злую истину. Относительно кривой имени Гаусса математики уверены, что это пришло из практики, в данном случае — из статистики измерений. Ну а практики метрологии точно знают, что такая функция мигрировала из математики. К обоюдному согласию и удовольствию ни те, ни другие этот вопрос не обостряют. Иначе такая фигня получится!
Реальность же такова: Для функций распределения есть особый аппарат ОПОЗНАНИЯ функции. По крайней мере — опознание характеристик функции. Сколько я этим занимался — Гаусса не было ни разу. То есть в ПРОМЫШЛЕННОСТИ существовала процедура опознания образа распределения. Потому, что промышленность — это реальность. Ну а в экономике такая процедура только помеха. Потому, что экономическая наука — реальностью НЕ является.
В атомной промышленности три случая Тримайл-Айленд, Чернобыль и Фукусима перевернули все нормы. Следующие АЭС будeт строить уже с учётом уроков.
Кто сказал, что последствия экономических кризисов менее ужасны? Но творцам таковых с рук сходит ВСЁ. Абсолютно всё. Страшные люди. Ещё страшнее система, которая без ТАКИХ решений и без таких специалистов жить не может. Выбор не велик. Или победит человечество (с чего бы это вдруг?), или победят экономисты.